Tsumego Paid Off: I Found a Weakness

I was watching the game of two of my friends from the American Yunguseng Dojang yesterday. Since it was not my own game I was a dispassionate observer. 

In my own games I see my own weaknesses, but miss the weaknesses of my opponent. Neither of these players was my opponent, and I had no weaknesses of my own to worry about, so I could see the game more clearly than I might view a game of my own.

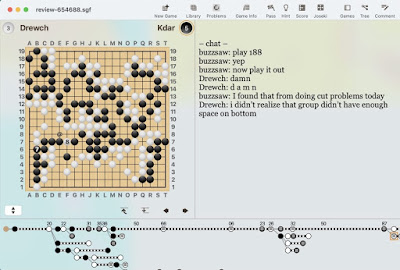
Earlier in the day I was working on a set of cut problems from 101 Weichi. I had been through those problems a number of times, and I was doing them again. I had been noticing in the problems that often a cut happens after a wedge. Once the wedge stone is placed into Atari, and saved, there remain two cuts. Only one of those cuts can be protected. Seeing this happen often in the problems makes it more likely to see it in one’s games.

During the game I saw such an opportunity for white. It did not matter from which side black gave Atari because both sides had two cuts. I was excited.

After the game was over I asked if we could take a look at it.

We came to conclusion that it worked.

The cut was worth making because there were black stones in the lower left that would not survive after the cut. It would have been Game Over. It was a comfortable victory for white as it was.

I was very proud of myself for finding this.

It turns out that white had been so concerned about his own weakness that he failed to see the weakness in black.

In-seong has told me that this is a big problem in my games. He says that I see the game from my side, and that I need to see the game from my opponent’s side.  Clossius focused this tendency right away too. 

Now that I can find a weakness as a dispassionate observer I need to calm down in my own games and find such weaknesses there.

An interesting aside... white dreamed about the cut that night.

If I can master the wedge perhaps I can live up to my name, buzzsaw.